Optimierung des Modells mittels Forecast Accuracy Kennzahlen
Aus dem ersten Teil der Reihe rund um die Nachfragevorhersage wissen wir nun, wie wir ein Simple Exponential Smoothing (SES) Modell für einen Artikel mit einer Bedarfsreihe erstellen können. Nun wollen wir uns dran begeben zu erfahren, ob unser Modell auch zu was taugt.
Zunächst entfliehen wir aber dem Detail um uns nochmals das große Ziel vor Augen zu führen. Unser Beispielunternehmen Feinkosthandel Rheinland verkauft etwas mehr als 3000 Artikel aus verschiedenen Lagern, für die wir sofern möglich eine Nachfragevorhersage erstellen möchten, die relativ nah am Optimum ist. Für ein einzelnes Beispiel, wie in Teil 1, kann man sicherlich per Trial & Error herausfinden, welcher alpha Wert die beste Prognose erzeugt, aber für 3000 wird es dann schon schwieriger und wir benötigen einen Algorithmus, der uns bei der Erstellung hilft. Und genau diesem müssen wir beibringen zu wissen was ein guter Forecast ist.
An dieser Stelle kommen nun endlich die Forecast Accuracy Kennzahlen ins Spiel. Auch hier werde ich nur einen Bruchteil der, im Supply Chain Management angewandten Kennzahlen präsentieren und empfehle Ihnen darüber hinaus andere Quellen zu bemühen, um sich ein gutes Gesamtbild zu machen. Wie kehren zu unserem Detail und damit unserem Beispiel zurück.
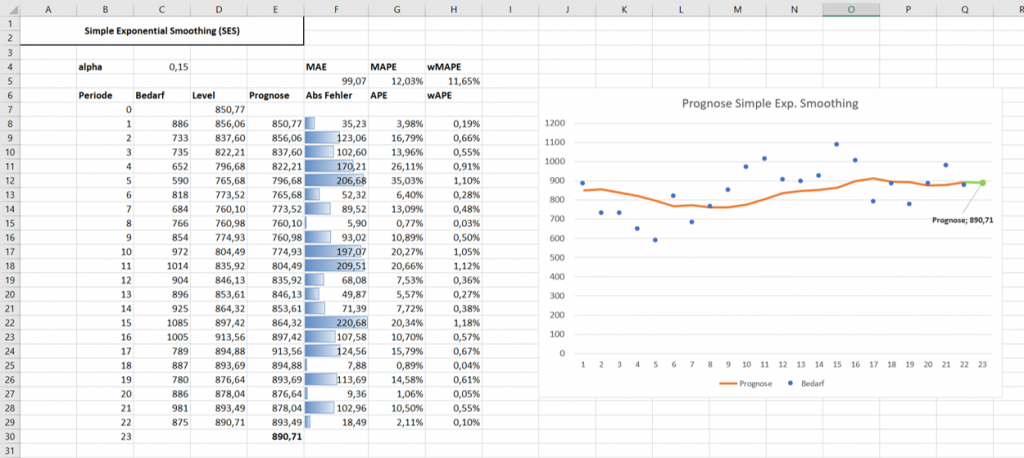
Der Fokus soll diesmal auf den Spalten F bis G liegen. Vorab werde ich die einzelnen Parameter kurz erklären:
- Abs Fehler (Spalte F)
- Der absolute Wert des Fehlers aus Bedarf – Prognose
- APE (Absolute Percentage Error) (Spalte G)
- Die absolute prozentuale Abweichung der Prognose im Verhältnis zum Bedarf
- wAPE (weighted Absolute Percentage Error) (Spalte H)
- Die gleiche Kennzahl wie zuvor, jedoch diesmal gewichtet an der Gesamtsumme des Bedarfs
- Wozu das wichtig ist, finden wir im späteren Verlauf des Posts heraus.
Wie sich die einzelnen Werte der Spalten errechnen, können Sie einfach aus der Beispieldatei entnehmen, sodass ich jetzt nicht weiter beschreiben muss, wie diese zu Stande kommen. Wenn Sie die Datei zum ersten Mal öffnen, bekommen Sie den Hinweis, ob sie die Makros aktivieren möchten. Dies bejahen Sie bitte, sodass Sie ihre eigenen Versuche durchführen können. Lassen Sie uns aber einen Blick in die Logik der Werte werfen und wie diese in eine Kennzahl verwandelt werden können.
Der Abs Fehler zeigt uns, um wie viel Stück wir mit unserer Prognose neben dem Bedarf lagen. Daraus ergibt sich die Kennzahl MAE (Mean Absolute Error), zu deutsch mittlerer absoluter Fehler. Im Schnitt scheinen wir also gut 99 Stück Fehlerquote in der Prognose zu haben. In Prozentwerten ausgedrückt erschließt sich der APE, der die Verfehlung in Prozent ausdrückt und in der Kennzahl MAPE (Mean Absolute Percentage Error), durchschnittliche prozentuale Abweichung, wiederverwertet wird.
In der Praxis findet der MAPE oft Anwendung, wir werden aber in Kürze sehen warum dieser, wie viele andere Kennzahlen auch, sein Schwächen hat. Man könnte an dieser Stelle einer üblichen Praxis-Vorgehensweise folgen und bestimmen, dass das SES-Modell einen möglichst geringen MAPE haben soll. Da die Formel des Simple Exponential Smoothing, als einzige Felxibilität den alpha Wert hat, können wir auschließlich diese Stellschraube verwenden, um den MAPE zu verringern. Sie bedenken, dass wir das nur bis zu einem aplha von <=0,25 tun möchten! Best practice!
Wie eingangs erwähnt können wir uns jetzt auf den Probieren wir es mal aus! Weg begeben, den wir aber vorerst vermeiden!
Zunächsteinmal widmen wir uns dem wAPE. Wie der Name schon verrät, gewichten wir die prozentuale Verfehlung am Gesamtbild des Bedarfes. Formel ist im Arbeitsblatt. Dadurch erhalten wir die Kennzahl wMAPE (weighted Mean Absolute Percentage Error), die eine Summe der wAPE ist.
Warum benötigen wir eine Gewichtung?
Das Verfahren des wMAPE ermöglicht es uns, Ausreißer und deren Auswirkung im Bedarfsbild in gewisser Weise abzufedern und somit eine robustere Kennzahl zu schaffen.
Gehen wir in unserem Bedarfsbild beispielsweise davon aus, dass in Periode 10 & 11 ein Großkunde, der 85% des monatlichen Bedarfs des ausgewählten Artikels ausmacht einen Brand in seinem Lager hatte und uns demnach der Bedarf weggebrochen ist. Der MAPE reagiert auf den Bedarfseinbruch mit einer 36%-igen Erhöhung des Forecastfehlers, wohingegen der wMAPE nur 10% steigt und die Ausreißer besser verträgt.
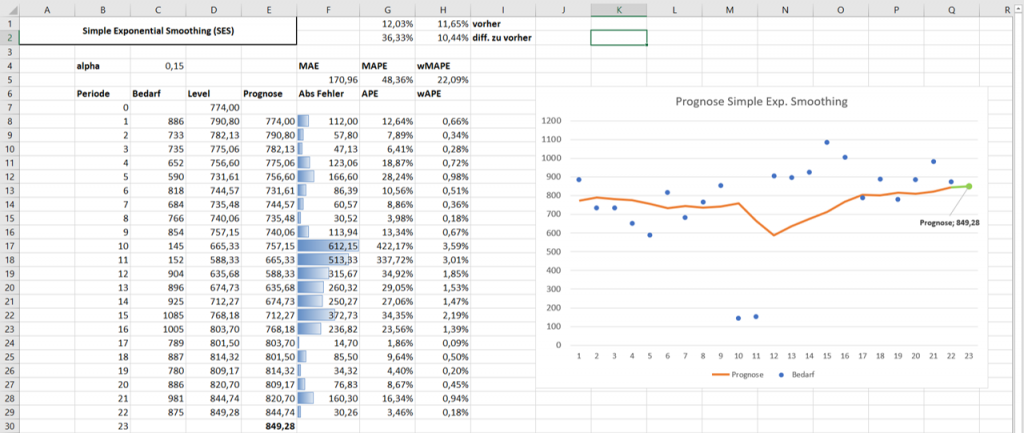
Da der Großkunde nun seine Präventivmaßnahmen gegen Brände verstärkt und ein weiteres Ausweichlager unter Vertrag genommen hat, gehen wir für die Zukunft davon aus, dass sich ein solches Ereignis nicht zwingend wieder ereignet. Daumen sind gedrückt!
Rein von der Logik her, wird sich demnach das SES Modell weiterhin bewähren. Würden wir für unseren Optimierungsalgorithmus nun aber mit dem MAPE arbeiten und dieser eventuell ein anderes Forecastmodell als besser empfinden könnte dieses, dank geringerem MAPE gewinnen, jedoch aus unserer Sicht völlig ungeeignet sein. Ein gewichteter wMAPE von gut 22% ist immer noch ein gutes Maß für unser Modell.
In einem weiteren Arbeitsblatt der Datei finden Sie außerdem ein weiteres Beispiel, dass den MAPE genauer betrachtet. Sie sehen, dass trotz gleichem MAE der Mape des Forecasts mit der geringeren prognostizierten Mengen besser abschneidet! Der wMAPE hingegen ist neutral.
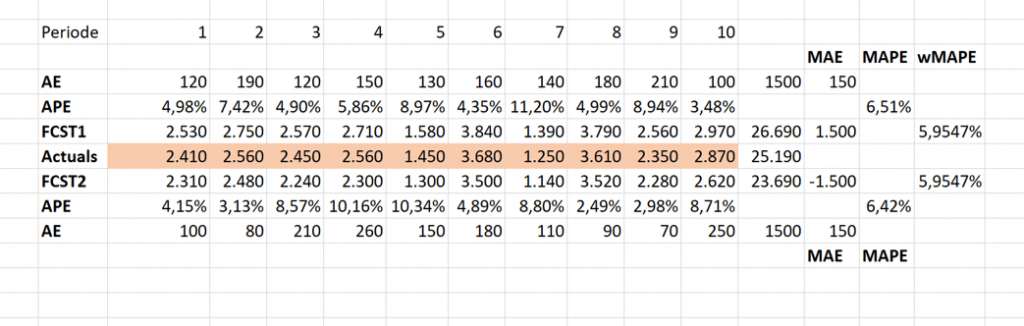
Das Beispiel des Absatzeinbruchs zeigt, dass verschiedene Forecast Accuracy Kennzahlen zu unterschiedlichen Ergebnissen kommen und demnach einen Einfluss auf die Nachfragevorhersage und das selektierte Modell haben. Behalten Sie das stets im Hinterkopf und überprüfen Sie ihre Kennzahlen in regelmäßigen Abständen, probieren neue Wege aus, um stets das bestmögliche Modell zu erhalten.
Erstellen des Nachfragevorhersage-Algorithmus mit VBA
An dieser Stelle möchte ich damit beginnen langsam in die VBA Entwicklungsoberfläche zu wechseln und im Ansatz durch den VBA Code, bzw. die einzelnen Programme zu führen, die uns helfen das SES Modell mit dem geringsten wMAPE zu identifizieren und für jedes einzelne Material durchzulaufen.
Der Code besteht dabei aus drei Programmen, die aufgerufen und nach und nach durchgeführt werden. Mit der Besipieldatei können Sie dann ausprobieren und somit ihre eigenen Werte forecasten.
Der erste Teil des SES-VBA Programms ruft in der Schleife ein anderes Programm ForecastingLine auf. Zunächst wird aber das Arbeitsblatt TestData aktiviert, sowie die letzte Reihe bestimmt, sodass auch für alle eingepflegten Produkte ein Simple Exponential Smoothing durchgeführt wird. Zu Beginn wird außerdem ein Timer gestartet, sodass wir am Ende wissen, wie lange der Code lief. Kurz vorab – für die 500 eingepflegten Testreihen läuft der Code gut 2,5 Sekunden.
Sub ForecastingFullexpSmoothing()
'Das Hauptprogramm des ExpSmoothing ruft die ForecastingLine Prozedur auf,
'die wiederum die SimpExpSmoothing aufruft, wo das eigentliche Forecasting durchgeführt wird
start = Timer()
ThisWorkbook.Worksheets("TestData").Activate
lrow = ActiveSheet.Cells(Rows.Count, 3).End(xlUp).Row
For j = 2 To lrow
Call ForecastingLine
Debug.Print wMAPE & "-" & alpha
Next
Debug.Print (Timer() - start)
End SubSpringen wir nun in das zweite Programm ForecastingLine. Hier beginnen wir damit einige Variablen zu deklarieren und unser Inkrement festzulegen mit dem wir die einzelnen alpha Werte hochzählen. Wir beginnen mit einem alpha von 0,05 und zählen in 0,025 Schritten nach oben. der new_wMAPE Wert wird zunächst auf 9 gesetzt, sodass das Modell einen initialen Vergleichswert hat.
Beginnend mit ReDim expArr füllen wir ein VBA Array, was im Grunde genommen einen virtuelle Tabelle ist, mit den tatsächlichen Verkaufen der beobachteten Perioden, sodass wir schon mal die Basis für das SES-Modell haben. In der darauffolgenden Schleife wird dann der dritte Codeabschnitt ausgeführt, der die eigentliche Arbeit verrichtet. Bevor wir dahin springen, gehe ich noch auf einen Bestandteil der Schleife ein, der ermittelt, ob der neue wMAPE mit gesetztem alpha Wert besser ist als der vorige, denn nur dann wir dieser alpha Wert gespeichert und für den letzten Durchlauf verwendet, um nachher den Forecast in “Periode 23” auszugeben.
Sub ForecastingLine()
Dim a, b, x As Long
Dim start As Long
Dim new_wMAPE As Double
Dim new_alpha As Double
'Hier kann man die schrittweise Folge der Alphas einstellen
'Bsp bei a = 0.025 muss die Schleife 9 (b) Mal durchlaufen werden um auf 0.25 zu kommen
'new_wMAPE als Startwert, sodass dagegen verglichen werden kann
a = 0.025
b = 9
alpha = 0.05
new_wMAPE = 9
ThisWorkbook.Worksheets("TestData").Activate
lrow = ActiveSheet.Cells(Rows.Count, 1).End(xlUp).Row
lcol = ActiveSheet.Cells(1, Columns.Count).End(xlToLeft).Column
period = Application.WorksheetFunction.Count(Range(Cells(1, 1), Cells(1, lcol)))
ReDim expArr(period + 1, 6)
'Hier wird das Array mit den Actuals und der Periode gefüllt und dabei transponiert
expArr(0, 0) = 0
For i = 1 To period
expArr(i, 0) = Cells(1, i + 2)
expArr(i, 1) = Cells(j, i + 2)
Next
'Durchlaufen aller ExpSmoothing Möglichkeiten mit den verschiedenen alpha-Werten
For x = 1 To b
Call SimpleExpSmoothing
'Suchen nach dem kleinsten wMAPE mit dazugehörigem alpha
If wMAPE < new_wMAPE Then
new_wMAPE = wMAPE
new_alpha = alpha
End If
alpha = alpha + a
Next
'Hier wird das alpha mit dem besten wMape selektiert und dann als Wert für den letzten Durchlauf der Reihe genommen
alpha = new_alpha
Call SimpleExpSmoothing
ActiveSheet.Cells(j, 25) = expArr(23, 3)
End SubVorerst muss aber natürlich das durchgeführt werden, was wir vorher in mühsamer Kleinstarbeit an einem Beispiel durchgegangen sind und auf ich an dieser Stelle nicht allzu ausführlich nochmals eingehen möchte. Alle Parameter wie AE (Absolute Error), APE (Abolsute Percentage Error), wAPE (weighted Absolute Percentage Error), MAE (Mean Absolute Error), MAPE und wMAPE (weighted Mean Absolute Percentage Error) werden hier für jedes eingespielte alpha durchlaufen und dann, wie zuvor erwähnt, in Forecasting Line überprüft und letztendlich ausgegeben.
Sub SimpleExpSmoothing()
'Simple Exponential Smoothing according to Chopra & Meindl's Supply Chain Management
Dim lrow, lcol As Long
Dim L0 As Double
'Dim aplha As Double
Dim MAE As Double
Dim APE As Double
Dim MAPE As Double
Dim wAPE As Double
'Calculate the Level (L0) // beim Index ist die Spalte ausm Array+1
With Application.WorksheetFunction
L0 = .Average(.Index(expArr, 0, 2))
End With
'Calculate the remaining Levels
expArr(0, 2) = L0
For i = 1 To period
expArr(i, 2) = expArr(i, 1) * alpha + (1 - alpha) * expArr(i - 1, 2)
Next
'Calculate the Forecast // Basically offset the Level
For i = 1 To period + 1
expArr(i, 3) = expArr(i - 1, 2)
Next
'Calculate the AE (Absolute Error) |Actuals-Forecast|
For i = 1 To period
expArr(i, 4) = Abs(expArr(i, 1) - expArr(i, 3))
Next
'Calculate the MAE (Mean Absolute Error)
With Application.WorksheetFunction
MAE = .Average(.Index(expArr, 0, 5))
End With
'Calculate the APE (Absolute Prcentage Error) |Actuals-Forecast|/Actuals
For i = 1 To period
expArr(i, 5) = expArr(i, 4) / expArr(i, 1)
Next
With Application.WorksheetFunction
MAPE = .Average(.Index(expArr, 0, 6))
End With
'Calculate the wAPE (weighted Absolute Prcentage Error) Actuals * APE / Sum(Actuals)
With Application.WorksheetFunction
For i = 1 To period
expArr(i, 6) = expArr(i, 1) * expArr(i, 5) / .Sum(.Index(expArr, 0, 2))
Next
wMAPE = .Sum(.Index(expArr, 0, 7))
End With
End SubAm Ende des Durchlaufs haben wir, in diesem Fall in Splate Y, für jede Linie ein Forecast Ergebnis mit dem geringsten wMAPE. Wunderbar!
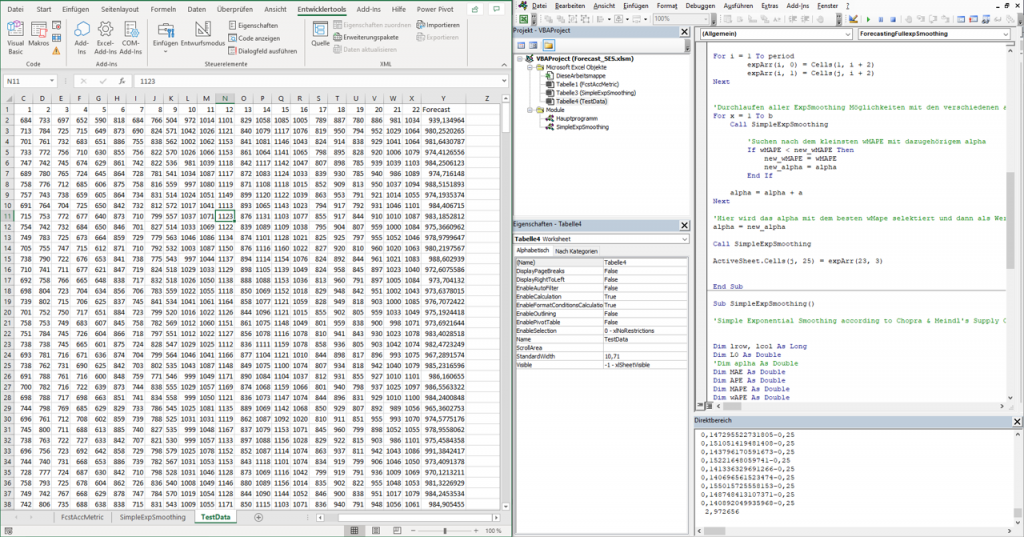
Abschlussgedanken und Ausblick
Mit der Erstellung des VBA-Programms und durchlaufen des SES-Modells haben wir einen gemeinsamen Grundstein für mögliche Erweiterungen gesetzt. Sicherlich ist das Bedarfsbild in der Praxis, besonders bei einem großen Produktportfolio, weitaus differenzierter als ich in meiner Beispieldatei darstellen konnte. Aber ich denke, dass ich Ihnen einen guten Einblick geben konnte, wie so etwas aussehen könnte.
Um das Programm als solches noch leistungsfähiger zu machen, müssten natürlich noch weitere Forecast-Varianten eingepflegt werden, die beispielsweise starke Trends oder Saisonalitäten berücksichtigen. Das würde ermöglichen ein breites Spektrum an Materialien mit einer Prognose zu beschenken. Was man allerdings bedenken muss ist, dass in der Praxis nicht alle Produkte für einen Foreacst geeignet sind, weil sie einfach zu sporadisch verkauft werden oder die Volatilität zu hoch ist. In einem späteren Post werde ich mich damit befassen, wie man ein Portfolio klassifiziert und somit einfach erkennen kann, welche Produkte geeignet sind und welche nicht.
Bis dahin, bleiben Sie erfolgreich!
#Zusatzinformationen Link zu einem Video, dass sich u.a mit wMAPE beschäftigt.
#Link Beispieldatei




No responses yet