Neue Daten, Kennzahlen und deren Berechnung
Wichtige Kennzahlen und KPIs (Key Performance Indicator(s)) ranken sich im Supply Chain Management (SCM) um: die Lagerbestände. In dieser Reihe werden uns mit einigen dieser befassen und sie berechnen, um uns letztendlich einen besseren Überblick über diesen Baustein des SCM machen zu können.
Als ersten Teil dieser Reihe gebührt es sich natürlich kurz vorzustellen und eine Vorschau zu geben, auf das was in der nächsten Zeit rund um das Thema Lagerbestandsmanagement ansteht. Ich möchte mich dabei an unserem bisherigen Datenmodell aus dem E-Book orientieren und dieses erweitern. Die neue Tabelle ist eine Bestandsdatei unseres Beispielunternehmens Feinkosthandel Rheinland vom 30.09.2019.
Sicherlich gibt es eine schier unbegrenzt scheinende Anzahl an Kennzahlen für das Lagerbestandsmanagement, die ich alle gerne behandeln würde, andere Themen dann aber zu kurz kämen, was ich sehr gerne verhindern möchte. Als Startpunkt nutze ich eine kleine Sammlung, die sich an das Buch Supply Chain Management von Sunil Chopra und Peter Meindl anlehnt. (Thalia)
- Lagerbestandsreichweite
- Lagerumschlagshäufigkeit
- Produkte, die über eine definierten Zahl DoD (Days of Demand) liegen
- Durchschnittliche Nachschublosgröße
- Anzahl der Tage, die ein Produkt nicht im Lagerbestand war
- Obsoleter Bestand
Alles schöne Kennzahlen, die theoretisch relativ einfach zu errechnen sind wenn man von Einzelbeispielen ausgehen möchte. Leider habe ich es in der beruflichen Praxis zu oft erlebt, dass die Theorie aus allen nur so rausprudelte, die wahnwitzigsten Kennzahlen und Sägezahndiagramme (Grafik) benannt, alle in Gänze erläutert und auf den Punkt dargeboten wurden.
Leider wurde es dann immer dünner, wenn es um die Berechnung der Zahlen für ein Portfolio von mehreren tausend Artikeln in einem mehrstufigen Distributionsnetzwerk ging.
Genau dieses Problem werden wir in unserem Beispiel mit Power Pivot lösen!
Für viele der oben genannten Kennzahlen benötigt man den durchschnittlichen Lagerbestand. Da wir aktuell aber nur eine Bestandsdatei haben, wird das ein eher schwieriges Unterfangen. Die Kennzahl der Stunde und an dieser Stelle wird für uns die Lagerbestandsreichweite sein. Dazu benötigen wir den aktuellen Bestand, sowie die durchschnittliche Verkaufsmenge auf Tages/Wochen oder Monatsbasis. In unserem Fall fangen wir mit der geringsten Granularität, Tag an.
Erweiterung des Datenmodells
Fügen wir nun 20190930_Bestand.xlsx hinzu. Link zur Beispieldatei. Das Passwort der Datei ist das erste Wort bei Abb. 5-b im E-Book. Diese beinhaltet neben der Materialnummer und dem Distributionsknoten drei verschiedene Bestandsarten, wobei für uns der freie Bestand von Interesse ist. Unser erweitertes Datenmodell sieht nun so aus:
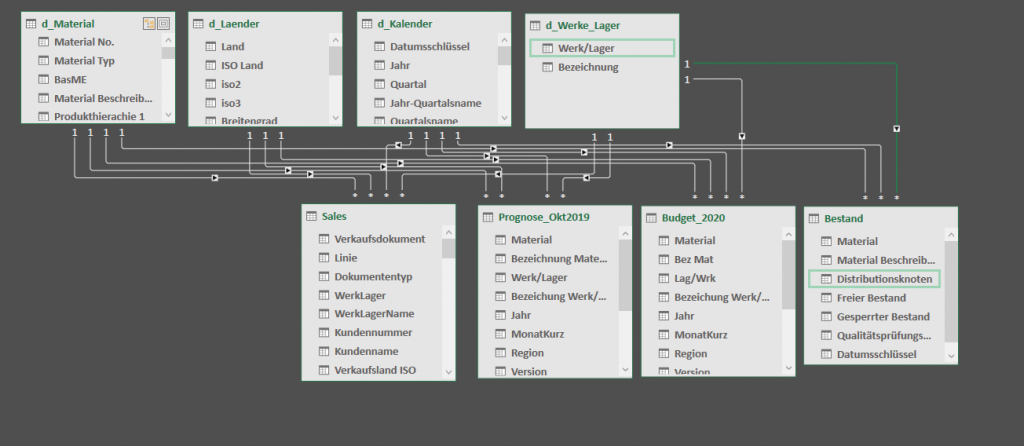
Um zu ermöglichen, dass die Bestandstabelle trotz nicht vorhandener Datumsspalte eine Beziehung mit unserem Kalender eingehen kann, habe ich eine Berechnete Spalte am Ende der Tabelle hinzugefügt. Diese enthält die Formel = DATE ( 2019; 9; 30 ). Das ist an dieser Stelle ein kleiner Trick, den man auch eleganter lösen kann. Auch das ist Thema eines meiner nächsten Posts.
Summe des freien Bestands als Measure
Nahezu jede neue Tabelle benötigt selbstverständlich ein oder mehrere Measures. Wir beginnen mit der Summe der freien (fr) Lagerbestände (LB) in Stück (ST):
[frLB_ST] = CALCULATE ( SUM ( Bestand[Freier Bestand] ) )
Damit ist der erste Teil der Aufgabe schon erledigt, einfacher geht es fast nicht. Das oben aufgeführte Measure dient uns nachher als Zähler in einem Bruch, der die Days of Demand also die Lagerbestandsreichweite in Tagen ausgeben wird.
Durchschnittliche Auftragsmenge pro Tag
Lassen Sie uns für den Moment kurz über das Ziel dieser Übung reden. Am Ende möchte ich eine PivotTable erzeugen, die uns die Produkte pro Distributionsknoten mit den dazugehörigen Lagerbestandsreichweiten ausgibt, die man dynamisch filtern und somit verschiedene Perspektiven einnehmen kann. Diese Dynamik erlaubt es auch auf Anfragen verschiedenster Art flexibel zu reagieren, ohne die gesamte Datei neu erstellen zu müssen. Lassen Sie das sacken.
In meinem E-Book haben wir das benötigte Measure bereits erstellt, ich gehe an dieser Stelle aber noch mal bündig darauf ein. Die Kalendertabelle d_Kalender hat als geringste Granularität und gleichzeitig Verknüpfungspunkt den Datumsschlüssel, der zu unserem Glück auf Tagesbasis angelegt wurde. Jede Linie der Tabelle repräsentiert somit einen Tag des Jahres.
Das Measure, dass wir an dieser Stelle recyclen wollen ist:
[ORD_ST] = CALCULATE ( SUM ( Sales[Menge in Stueck] ) )
Um nun einen Durchschnittswert pro Tag zu erhalten, müssen wir mithilfe einer Iterationsfunktion arbeiten. In diesem Fall ist es AVERAGEX(), die wir über die Kalendertabelle laufen lassen.
Unser Measure sieht dann wie folgt aus:
[avg_ORD_ST/t] = CALCULATE ( AVERAGEX ( d_Kalender, [ORD_ST] ) ) )
Was passiert hinter den Kulissen des Measures? Man kann sich das so vorstellen, dass eine virtuelle Spalte an die Kalendertabelle angefügt wird, in die Zeile für Zeile die Auftragsmenge des Tages hineingeschrieben wird. CALCULATE führt hier eine Kontextumwandlung durch und zieht sich die Daten aus der Sales Tabelle in die Kalendertabelle, die als geringste Granularität den Tag hat. Da Sales auch Verknüpfungen zu d_Material und d_Werke/Lager hat, können wir in der späteren PivotTable auch weiterhin mit Parametern dieser Tabellen arbeiten. Unsere Beispielparameter sind:
- Material: 55027565 – Cabernet Sauvignon We 1L 373695 SE
- Lager: DE54
- Monat-Jahr: März 2019
Selbstredend betrachten wir später alle Produkte, aber für den Moment gehen wir Schritt für Schritt (debuggen) das Beispiel durch. Riskieren wir einen Blick:
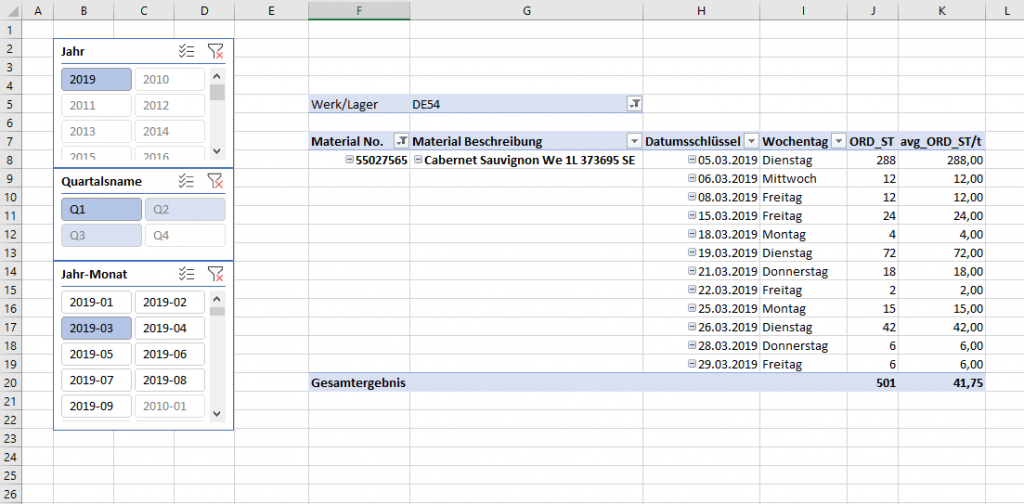
Nach kurzem Studium des obigen Screenshots kommen eventuell zwei Fragen in den Sinn:
- Der März hat 31 Tage, wir haben aber nur an 12 etwas verkauft, haben wir den korrekten Durchschnitt ausgerechnet?
- Im Beispiel gibt es zwar keine Verkaufsaufträge mit Mengen an Samstagen oder Sonntagen, aber wollen wir diese in unseren Durchschnitten überhaupt berücksichtigen?
Beantwortung der Fragen, ermitteln des verwendbaren Durchschnitts
Zugegeben, wenn ich schon so nachfrage hat es einen Hintergrund. Wir haben zwar einen Durchschnitt errechnet aber eigentlich nicht den, den wir haben möchten. Das soll sich ändern. Zur zweiten Frage bestimme ich, dass wir die Samstage, sowie Sonntage außen vorlassen. Es gibt zwar die Möglichkeit Kundenaufträge auf einen Samstag zu platzieren, das erlauben wir aber nur äußerst wenigen Kunden vom Feinkosthandel Rheinland und sonntags gäbe es wenn nur Fehleinträge. Aus diesem Grund würden uns die beiden Tage den Schnitt nur unnötig verwässern und uns wohlmöglich eine ungenaue Lagerbestandsreichweite bescheren.
Demnach benötigen wir ein Measure, dass die Tage an denen keine Auftragsmenge eingelastet war, mit einer “0” bestückt. Daraufhin können wir den Mittelwert dessen bilden und haben dann die tatsächliche Durchschnittsmenge des Produkts.
Unser zuvor erstelltes Measure wollen wir von [avg_ORD_ST/t] auf [avg_ORD_ST] umbenennen. Im Grunde genommen errechnet dies die durchschnittliche Auftragsgröße des Produkts im ausgewählten Filterkontext. In unserem Fall Werk und Zeitraum.
Unser neues Measure mit altem Namen sieht nun wie folgt aus:
[avg_ORD_ST/t] =
CALCULATE (
AVERAGEX (
ADDCOLUMNS (
VALUES ( d_Kalender[Datumsschlüssel] ); “ORD”; [ORD_ST] + 0 );
[ORD]
)
)
Diese Verformelung hat schon ein anderes Kaliber als die beiden vorigen. Wir debuggen uns durch die Schritte und beginnen beim hellblauen VALUES und bewegen uns gen Norden. VALUES füllt den ersten Parameter von ADDCOLUMNS und erzeugt eine Liste von einzigartigen Werten der Spalte [Datumsschlüssel]. In unserem Fall also: das Tagesdatum. Dieser Spalte wird per ADDCOLUMNS eine weitere hinzugefügt, die den Namen ORD erhält. In dieser hinzugefügten Spalte befinden sich dann die Werte des Measures [ORD_ST]
| Datumsschlüssel | ORD |
| 01.03.2019 | Wert aus [ORD_ST] an dem Tag |
| 02.03.2019 | Wert aus [ORD_ST] an dem Tag |
AVERAGEX als Iterationsfunktion benötigt eine Tabelle als Input. Diese haben wir mit dem Einsatz von ADDCOLUMNS erzeugt, da diese Funktion als Ausgabewert genau diese liefert.
Im zweiten Teil von AVERAGEX bestimmen wir die Spalte die iteriert und gemittelt werden soll. Die Funktion geht demnach Zeile für Zeile ab, behält den Detailgrad Tag bei, auch bei späterer Verwendung in der PivotTable und ermittelt abschließend den Mittelwert. Den krönenden Abschluss macht CALCULATE, sodass wir PowerPivot und uns sagen, dass die Eigenschaften, die diese essentielle Funktion mitbringt aktiviert sind.
Zurück ins Studio und unserer PivotTable:
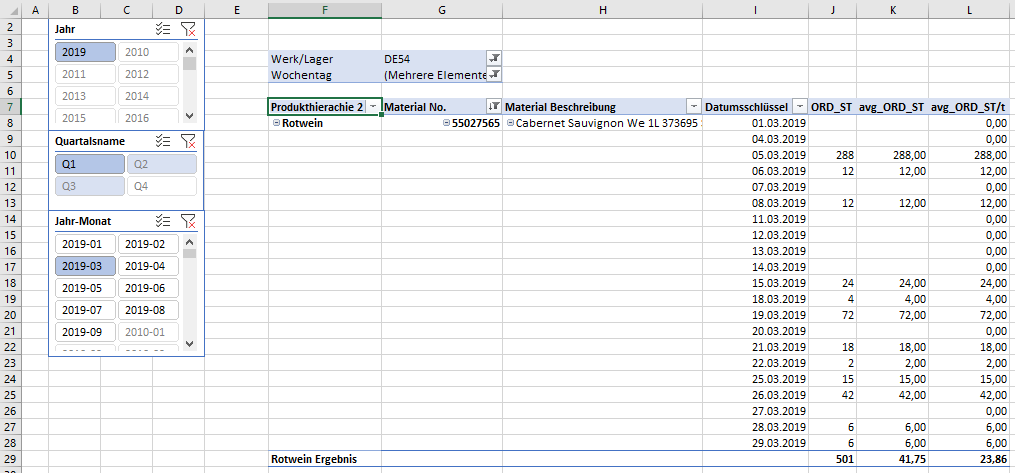
In dem obigen Beispiel sehen wir direkt die Wirkweise des neuen Measures. Es verhält sich tatsächlich wie wir es vorgesehen hatten. Ich habe außerdem die Wochentage Samstag und Sonntag im Berichtsfilter entfernt. Der 1. März 2019 war ein Freitag. Wir sehen also, dass im März 2019 die durchschnittliche Auftragsgröße 41,75 Stück war und wir 23,86 Stück im Schnitt täglich verkaufen. Wunderbar, an dieser Stelle vertrauen wir Power Pivot, dass die Measures auch bei allen anderen Produkten richtig arbeiten, nehmen den Datumsschlüssel aus der PivotTable, lösen den Monats- sowie Materialfilter, sodass wir die Werte aller Materialien sehen.
Zu guter Letzt möchten wir natürlich unsere Lagerbestandsreichweite pro Material sehen und erzeugen unser Days of Demand (DoD) Measure:
CALCULATE ( DIVIDE ( [frLB_ST], [avg_ORD_ST/t] ) )
DIVIDE als Funktion hilft dabei ein Teilen durch 0 abzufangen und ist in ihrer Tätigkeit schneller und klarer als eine IF-Verschachtelung.
Ich habe mir die Freiheit rausgenommen für eine letzte Ansicht unserer Arbeit die Produkthierarche 2 = Gin zu filtern. Hier soll es nicht bei jedem Beispiel um Alkohol gehen, aber die Produktgruppe beinhaltet eine übersichtliche Anzahl an Produkten.
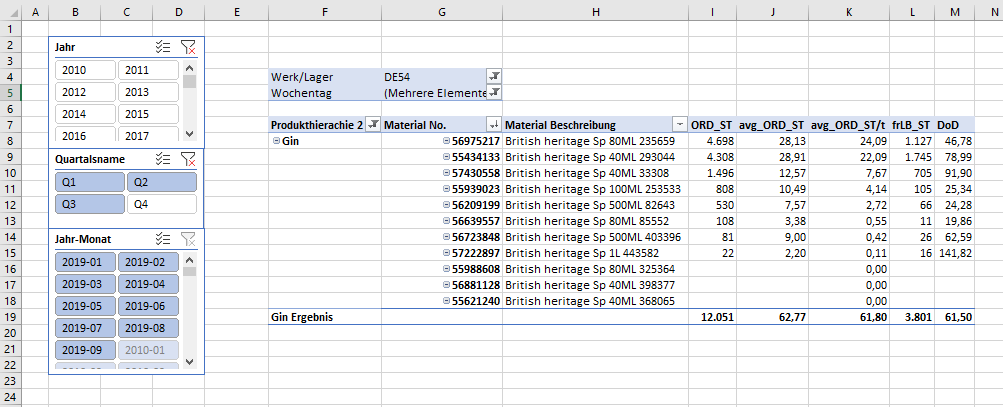
Als Überprüfungsmeasure habe ich noch unser anfänglich erstelltes [frLB_ST] in die Tabelle überführt. Unsere aktuelle Übersicht zeigt, dass wir beispielsweise bei dem ersten Produkt der PivotTable eine Lagerbestandsreichweite von gut 47 Tagen haben. Wir haben nun die Möglichkeit in allen unseren Standorten zu prüfen, wie weit wir mit unseren freien Beständen theoretisch kommen würden und ob unser Distributionsnetzwerk ausgeglichen, oder eventuell an der ein oder anderen Stelle überfrachtet bzw. unterliefert ist.
Der aufmerksamen Leserin, dem aufmerksamen Leser werden die Teilergebnisse unserer Produktgruppe Gin aufgefallen sein und dass sich diese im Gegensatz zu einer normalen PivotTable eventuell komisch verhalten.
Die Erklärung dessen wird in einem der nächsten Posts folgen, bis dahin: Viel Erfolg bei ihrer Datenanalyse!
#Formelwissen: ADDCOLUMNS ; VALUES ; CALCULATE ; AVERAGEX ; DIVIDE




2 Responses
Moin Marcel,
Dein Buch sieht gut durchdacht aus. Ich freue mich darauf, etwas von Deinem Wissen aufzusaugen.
Beste Wünsche für dein E-Book!
VG
Eric
Hi Eric,
ich hoffe, dass es dir den Einstieg ermöglicht und du schnell Erfolge erzielst. Viel Spaß und wenn du Fragen hast, gerne melden.
Gruß,
Marcel